1. 机器学习的一般步骤

1. 确定假设函数h(x)

这一步需要确定我们常说的机器学习的模型，模型的好坏决定了我们机器学习的效果的好坏。我们可以选择线性模型，也可以选择非线性模型。我们通常选择的模型通常为了解决两大类问题：一类是回归问题，这种模型一般用来预测结果是连续型的数值的情况；另一类是分类问题，这种模型一般用来预测结果是离散型的有限多个的情况

2. 确定代价函数（cost function）

代价函数是定义在整个数据集上，计算样本误差平均值的函数。通俗来讲，它的主要作用是衡量机器学习模型对样本拟合的程度。我们一般都会通过最小化代价函数的方法（预测值与真实值的误差最小）来求取模型参数。我们把代价函数取得最小值时所求得的模型叫目标函数 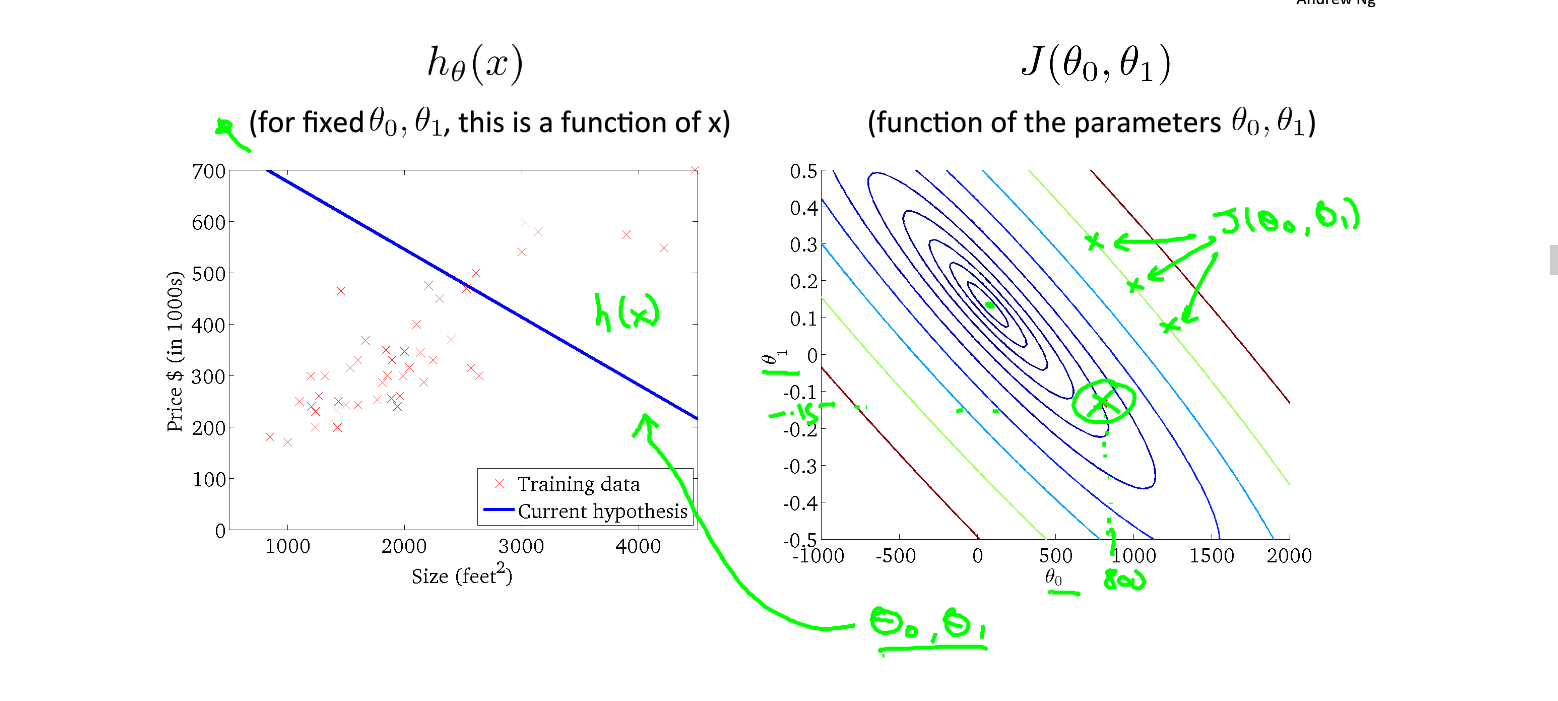上图显示了代价函数对函数模型的指导意义，当我们的代价函数取得上图二绿点所示的值时（这时，代价函数并未取得最小值），我们根据代价函数确定了模型的参数，画出的模型函数如上图一所示。这时我们可以明显发现我们的模型并未对数据做出最好的预测

3. 确定优化算法，训练模型

优化算法具体来讲就是采用什么样的算法来求得代价函数取得最小值时的模型参数的数值，训练模型指通过不断的迭代来一步步减小代价函数的值直至模型收敛。梯度下降算法是使用的非常广泛的求解目标函数的算法

4. 预测

此时我们已经将我们的模型训练至较好的水平，可以对数据做较好的预测

2. 算法推导

1. 线性回归的函数模型

上图第一个公式是线性模型的一般形式，上图第二个函数给出了线性模型的矩阵表示形式

2. 代价函数

线性回归的代价函数算法叫最小二乘算法，公式如下图所示

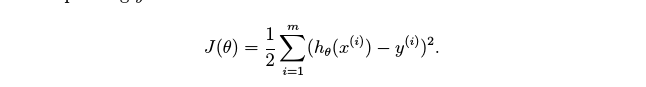
下面我将说明最小二乘算法的来源： 先回到我们一开始的地方，我们说回归问题解决的是预测结果是连续型变量的问题，而符合连续型变量的分布可以用高斯分布来描述。因为根据极限中心定理：多个独立随机变量的分布近似于高斯分布，而回归问题的特征变量可以认为是独立随机的，因此，我们可以认为回归问题的分布可以用高斯分布来描述。 高斯分布的概率密度函数公式如下图 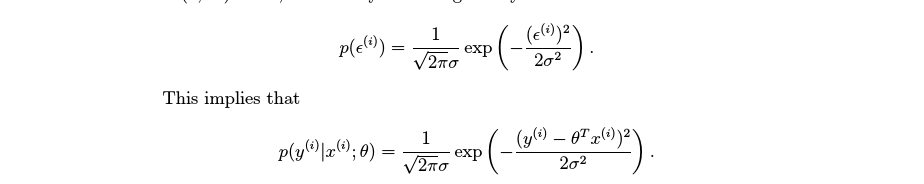它是一个钟形曲线，为了获取给定数据时，最可能的结果值，我们会计算给定x时，y的最大似然估计值

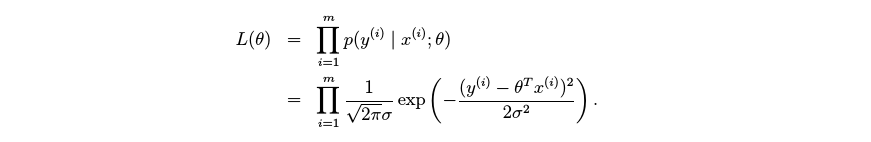
为了方便求出最大似然估计值，我们对似然估计取对数（不影响函数单调性和凹凸性）

以上是似然函数取对数之后的运算结果。倒数第二行中的第一项是常数项，对函数的最大值和最小值没有影响因此我们略去此项，方差的倒数也是常数项也不会影响函数的最大值和最小值，我们也略去。最后我们可以得出最小二乘的算法，即：要获取给定x，y最可能的取值就是要求的代价函数的最小值。

3. 梯度下降算法

梯度下降算法的核心是 $\theta_j:=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$

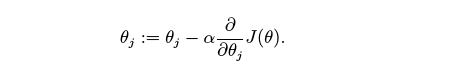
4.矩阵运算

下面将给出将梯度下降标量运算转换成矩阵运算的推导过程，矩阵运算可以极大地简化我们的程序开发难度

3. python代码实现

  # 梯度下降算法计算参数
  # alpha 步长 
def gradient_descent(x, y, alpha):
    x = np.mat(x)
    y = np.mat(y)
    m, n = np.shape(x)
    weigh = np.ones((n, 1))
	grad = np.ones((n,1))
    while la.norm(grad) > 10E-6::
        h = sigmoid(x * weigh)
		grad = x.transpose() * (y - h)
        # 核心梯度下降算法
        weigh = weigh + alpha * grad
    return weigh